[机器学习课程小结][1/10]

最近在Stanford的网络课程学习了机器学习的课程，Andre Ng讲的灰常不错啊。每种算法对应的实例挺多的，推导也很详细，它基本用matlab实现。就是概率统计数理统计矩阵论方面的知识最近得补一补了，直接应用在编程语言编写某些函数也是挺头疼的，不错还是略有收获。总共20节，听完5节，做个小结。

[L1 Introduction]
凸优化理论隐式马尔科夫模型 O natation 学习型算法

1)Supervised Learning
回归问题 Regression 分类问题(x|y)(肿瘤大小|癌症良恶) 学习给定了标准答案的样本->分析新样本的可能性支持向量机Support Vector Machine
2)Learning Theory
3)Unsupervised Learning
挖掘聚类分析->图像分析和处理的应用像素处理 ICA Algorithm 鸡尾酒问题（不同声源声音分离）
4)Reinforcement Learning
决策分析

马可夫过程

在概率论及统计学中，马可夫过程（英语：Markov process）是一个具备了马可夫性质的随机过程。马可夫过程是不具备记忆特质的（memorylessness）。换言之，马可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。具备离散状态的马可夫过程，通常被称为马可夫链。马可夫链通常使用离散的时间集合定义，又称离散时间马可夫链。具有马尔可夫性质的过程通常称之为马尔可夫过程。

	可数或有限的状态空间	连续或一般的状态空间
离散时间	在可数且有限状态空间下的马可夫链	Harris chain (在一般状态空间下的马可夫链)
连续时间	Continuous-time Markov process	任何具备马可夫性质的连续随机过程，例如维纳过程

具有马尔可夫表示的非马尔可夫过程的例子，例如有移动平均时间序列。最有名的马尔可夫过程为马尔可夫链，但不少其他的过程，包括布朗运动也是马尔可夫过程。

隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

隐马尔可夫模型最初是在20世纪60年代后半期Leonard E. Baum和其它一些作者在一系列的统计学论文中描述的。HMM最初的应用之一是开始于20世纪70年代中期的语音识别。在1980年代后半期，HMM开始应用到生物序列尤其是DNA的分析中。此后，在生物信息学领域HMM逐渐成为一项不可或缺的技术。

HMM有三个典型(canonical)问题:
已知模型参数，计算某一特定输出序列的概率.通常使用forward算法解决.
已知模型参数，寻找最可能的能产生某一特定输出序列的隐含状态的序列.通常使用Viterbi算法解决.
已知输出序列，寻找最可能的状态转移以及输出概率.通常使用Baum-Welch算法以及Reversed Viterbi算法解决.

凸优化

凸优化，或叫做凸最优化，凸最小化，是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。凸优化在某种意义上说较一般情形的数学最优化问题要简单，譬如在凸优化中局部最优值必定是全局最优值。凸函数的凸性使得凸分析中的有力工具在最优化问题中得以应用，如次导数等。
凸优化应用于很多学科领域，诸如自动控制系统，信号处理，通讯和网络，电子电路设计，数据分析和建模，统计学(最优化设计），以及金融。在近来运算能力提高和最优化理论发展的背景下，一般的凸优化已经接近简单的线性规划一样直捷易行。许多最优化问题都可以转化成凸优化（凸最小化）问题，例如求凹函数f最大值的问题就等同于求凸函数 -f最小值的问题。

凸优化（凸最小化）问题可以用以下几种方法求解：
捆集法
次梯度法
内点法

[L2]Linear Regression线性回归 Gradient descent梯度下降 Normal equations正规化方程组（都需要矩阵变换知识）

{(x(i), y(i)); i =1, . . . , m}称作包含m个训练样本的训练集合

h是假设的模型，可以带有一定先验知识，也可以是推测类型。学习算法通过学习训练集合的样本，得到h假设中的一定参数，在新的样本中进行预测和他推理。若目标变量y是连续的，则这样的学习问题可归为回归问题；若目标变量y是离散的，例如可在{0,1}中取值的垃圾邮件归类、癌症可能性判定问题，则可归为分类问题。

假设h假设是线性的，则假设就是各个参数线性的代数和。其中θ和x均是向量。x中各向量分量是各自变因素的取值，θ是各个自变量分量的系数或权重。则机器学习算法的目的就是求这个假设函数h(x)与真实值y的最小值。评估标准J(θ)以各样本和预测值的差的平方的二分之一为准。（二分之一纯粹是为了后期的运算）

1. LMS（ Least mean square）算法

即最小均方算法。算法实质是自适应的纠错学习，在学习中纠正参数θ的取值，直到收敛。其中，运用的最多的是梯度下降算法（Gradient Descent）

算法步骤为：

a)选取一个初始参数向量，可令其为0向量

b)重复查找各方向梯度，沿着梯度下降最快的方向搜索

c)直到四周均比局部梯度大的局部最优点

算法的数学描述为（该式为原始式，即梯度下降的数学定义）：

：=与计算机编程中的赋值语句等同。α称作学习比率。则上式中J(θ)对θ求导的数学推导式为：

这里更新最上式，对于单个训练样本

对所有训练样本，沿着梯度方向不断计算直到收敛

该方法中，每一次梯度的计算都用到了每个训练样本，这种梯度下降的方法称为批梯度下降。由于这里的最优化问题只有一个全局，因此这里的局部梯度最优点即是全局的梯度最优点。此外还可以采取随机梯度下降，每次梯度的计算选取随机的样本点，这样收敛的速度更快，但可能永远不会收敛到最优点，但会集中在最优点附近。因而在训练样本较大时可以采用随机梯度下降。这是随机梯度下降算法的数学表达：这是利用批梯度下降算法计算的梯度直到收敛，可以注意到每一次步长是不一样的，步长可在学习中不断调节，越接近最优点步长越短。

2.正规化方程

梯度下降是一种求取价值函数J(θ)的方法，正规化方程是另一种方案。首先提到的是几个必要的矩阵知识：

f与向量A的映射关系中，对f进行求导的定义：

关于迹的一些定理：

迹的乘法交换：

迹和转置的迹；迹的加法结合；迹的数乘

迹与倒数相关：

上式中，B是n_m矩阵，f的定义是依赖m_n矩阵的函数f（A）的值等于AB的迹。其中f（A）中的A的含义是A矩阵的每一个矩阵分量。

将J(θ)写成矩阵形式，给定的训练集合定义成矩阵X（m*n）m是训练样本个数，n是每个训练样本的自变量分量。

则已知的结果也可以用矩阵表示，或者说是向量表示

假设h和y的向量差为

J(θ)则可以表示为：

可以看到，h-y利用了向量内乘的方式，即向量乘以向量的转置，得到的实际上是个一维矩阵即一个数。为了找到J(θ)的最小值，可利用矩阵的求导，并参考上式中迹与倒数相关第三条：

第三步骤中，利用到实数的迹也是它本身，第四步中用到了迹和迹的转置，第五步中的方法是利用迹与倒数相关第三条，将A的转置设为θ，B=B的转置=X的转置*X C=单位阵，带入公式即可。令上式为零，则求出导数为零时θ的取值。得到的方程称为正规化方程：

梯度下降

梯度下降法，基于这样的观察：如果实值函数 F(x)在点 (a,f(a)) 处可微且有定义，那么函数 F(x)在 a点沿着梯度相反的方向 -▽ F(a) 下降最快。

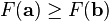因而，如果 $\mathbf{b}=\mathbf{a}-\gamma\nabla F(\mathbf{a})$ ,对于 $\gamma>0$ 为一个够小数值时成立，那么 $F(\mathbf{a})\geq F(\mathbf{b})$ 。

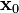考虑到这一点，我们可以从函数 $F$ 的局部极小值的初始估计 $\mathbf{x}_0$ 出发，并考虑如下序列 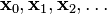$\mathbf{x}_0, \mathbf{x}_1, \mathbf{x}_2, \dots$ 使得

$\mathbf{x}_{n+1}=\mathbf{x}_n-\gamma_n \nabla F(\mathbf{x}_n),\ n \ge 0.$

因此可得到 $F(\mathbf{x}_0)\ge F(\mathbf{x}_1)\ge F(\mathbf{x}_2)\ge \cdots,$ 如果顺利的话序列 $(\mathbf{x}_n)$ 收敛到期望的极值。注意每次迭代_步长_ $\gamma$ 可以改变。假设 $F$ 定义在平面上，并且函数图像是一个碗型。蓝色的曲线是等高线，即函数 $F$ 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线的垂线。沿着梯度_下降_方向，将最终到达碗底，即函数 $F$ 值最小的点。